Структуры данных. Деревья

Это краткий дополненный конспект части о деревьях в книге Гид по Computer Science, Вильям Спрингер.

Основная информация

Дерево — это просто связный граф, не имеющий циклов. Назначаем одну вершину корнем дерева и определяем остальные вершины по их отношению к корню.

Пример дерева - DOM дерево.
Следующие определения для дерева равны между собой:

ациклический граф, в котором появится простой (без повторяющихся вершин) цикл, если добавить в него любое ребро;
связный граф, который перестанет быть связным, если удалить из него любое ребро;
граф, в котором любые две вершины связаны уникальным простым путем.

У дерева два типа узлов:

внутренние узлы - у которых есть хотя бы один дочерний элемент
листья - нет дочерних элементов

Ниже пример дерева с десятью вершинами и одним внутренним узлом.

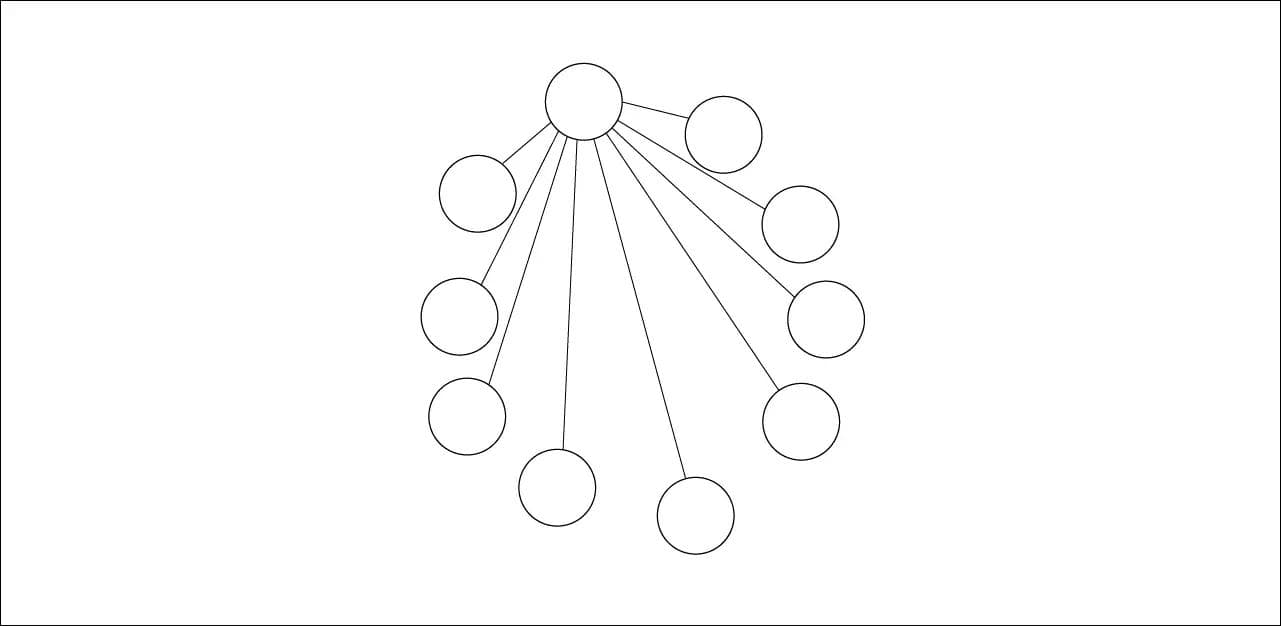
Кроме двоичных, широкое практическое применение имеют деревья с четырьмя узлами (дерево квадрантов). Они используются в геймдеве для организации сетки. Каждый узел в таком дереве представляет одно направление (север-запад, юго-восток и так далее).

Основные операции:

Добавление нового узла (add);
Удаление узла по его значению (remove);
Поиск узла по значению (find);
Обход всех элементов (traverse).

При необходимости этот список можно расширить более сложными алгоритмами:

Вставка/удаление поддерева;
Вставка/удаление ветви;
Вставка элемента в определенную позицию;
Поиск наименьшего общего предка для двух узлов.

Реализация на JavaScript

На основе массива

(Информация взята с этого сайта)

[3, 2, [3, 8], [[8], 3]];

Где

весь массив - корень.

элементы - дети.

ребенок не массив - лист, ребенок массив - внутренний узел со своими детьми

Как коллекция связных узлов

(Пример взят с этого сайта)

JavaScript

1class BinaryTreeNode {
2	constructor(value) {
3		this.left = null;
4		this.right = null;
5		this.parent = null;
6		this.value = value;
7	}
8
9	get height() {
10		let leftHeight = this.left ? this.left.height + 1 : 0;
11		let rightHeight = this.right ? this.right.height + 1 : 0;
12		return Math.max(leftHeight, rightHeight);
13	}
14
15	//При вставке важно обновить все затронутые ссылки: left или right для родительского узла и parent для дочернего. Если у родителя уже был потомок, его свойство parent нужно обнулить.
16
17	setLeft(node) {
18		if (this.left) {
19			this.left.parent = null;
20		}
21		if (node) {
22			this.left = node;
23			this.left.parent = this;
24		}
25	}
26
27	setRight(node) {
28		if (this.right) {
29			this.right.parent = null;
30		}
31		if (node) {
32			this.right = node;
33			this.right.parent = this;
34		}
35	}
36}
37let aNode = new BinaryTreeNode('a');
38
39let bNode = new BinaryTreeNode('b');
40aNode.setLeft(bNode);
41
42let cNode = new BinaryTreeNode('c');
43aNode.setRight(cNode);
44
45let dNode = new BinaryTreeNode('d');
46bNode.setRight(dNode);
47
48let eNode = new BinaryTreeNode('e');
49cNode.setLeft(eNode);
50
51let fNode = new BinaryTreeNode('f');
52cNode.setRight(fNode);

Двоичные деревья поиска

Двоичное дерево поиска (Binary Search Tree, BST) - корневое двоичное дерево (каждый узел имеет не более двух дочерних узлов).

Рекурсивно определяется:

ключ корня больше или равен ключу левого потомка (если он есть).
ключ правого потомка всегда больше или равен ключу корня.

Такая упорядоченность облегчает поиск элемента - можно отбросить неподходящую половину.

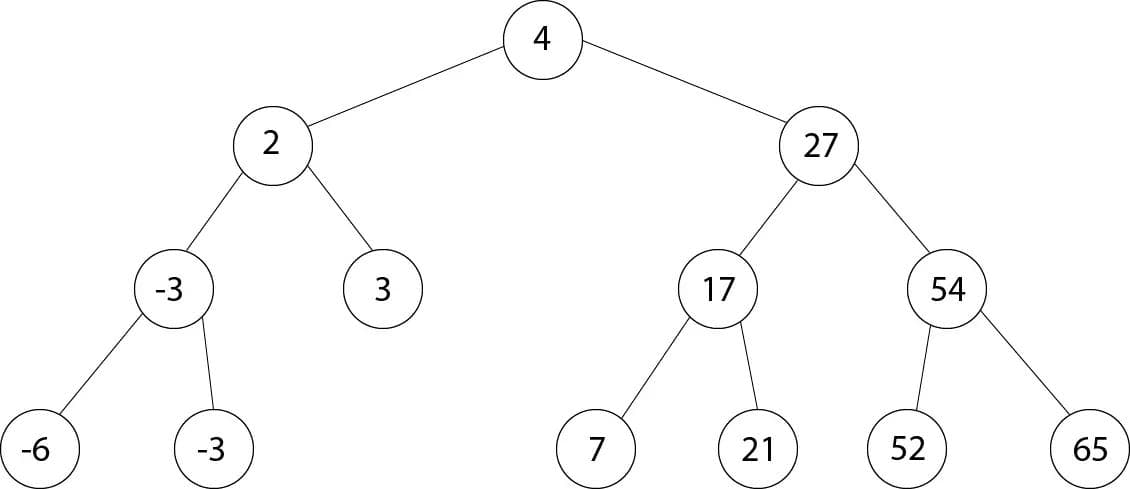
Время операций пропорционально высоте дерева - длине самой длинной цепочки от корня (высота которого равна нулю) до листа.

В общем случае это Θ(lg n).

Θ означает, что время выполнения ограничено как сверху, так и снизу; высота дерева должна быть не менее lg n.

в худшем случае (когда у каждого узла есть только один дочерний элемент, что, по существу, превращает дерево в связный список, несбалансированное двоичное дерево поиска) - O(n).

Ниже пример несбалансированного двоичного дерева.

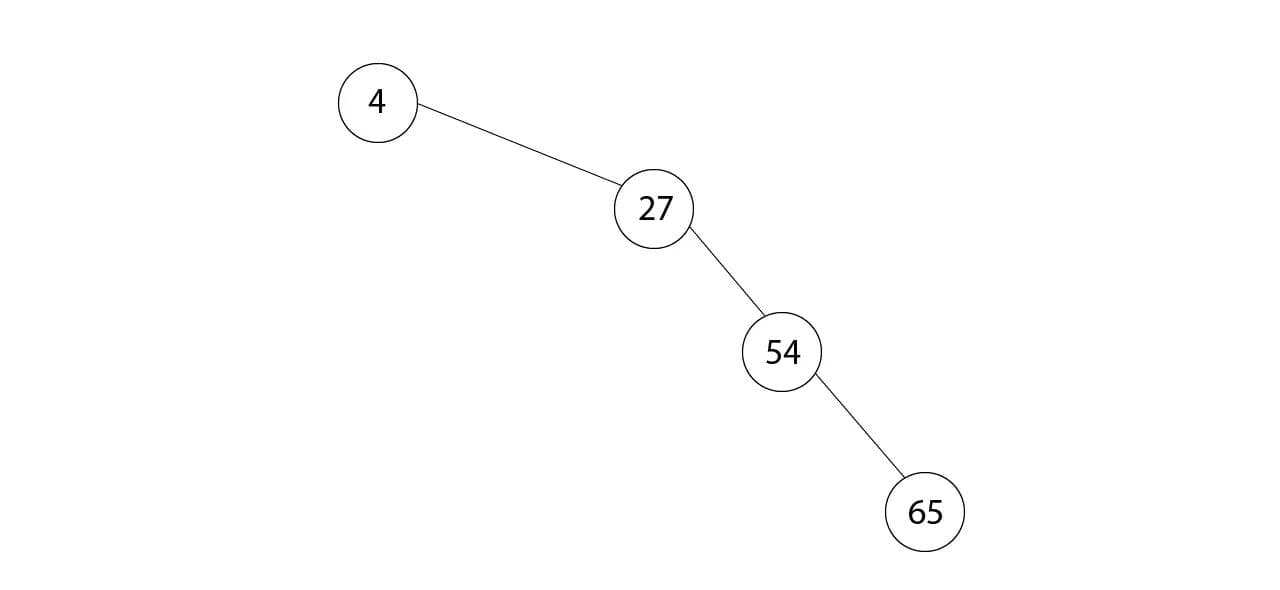
Двоичное дерево поиска может быть реализовано как коллекция связанных узлов - каждый узел имеет ключ и указатели на левый и правый дочерние элементы и на родительский элемент.

Реализация на JavaScript

Примеры взяты с этого сайта.

Первый добавленный узел становится корнем дерева.

Далее сравниваем значение нового элемента со значением родителя. Если оно больше помещаем элемент в левую ветвь, если меньше - в правую.

Добавление элемента

Строим дерево также, как и в предыдущем примере, только добавим новый метод добавления элементов, который сравнивает значения и отправляет элемент в нужную ветку.

JavaScript

1class BinarySearchTreeNode extends BinaryTreeNode {
2	constructor(value, comparator) {
3		super(value);
4		this.comparator = comparator;
5	}
6
7	insert(value) {
8		if (this.comparator(value, this.value) < 0) {
9			if (this.left) return this.left.insert(value);
10			let newNode = new BinarySearchTreeNode(value, this.comparator);
11			this.setLeft(newNode);
12
13			return newNode;
14		}
15
16		if (this.comparator(value, this.value) > 0) {
17			if (this.right) return this.right.insert(value);
18			let newNode = new BinarySearchTreeNode(value, this.comparator);
19			this.setRight(newNode);
20
21			return newNode;
22		}
23		return this;
24	}
25}
26
27class BinarySearchTree {
28	constructor(value, comparator) {
29		this.root = new BinarySearchTreeNode(value, comparator);
30		this.comparator = comparator;
31	}
32
33	insert(value) {
34		if (!this.root.value) this.root.value = value;
35		else this.root.insert(value);
36	}
37}
38
39const comparator = (a, b) => a - b;
40 /*если вернётся 0, значит, числа равны;
41если отрицательное число, значит, значение меньше искомого;
42если положительное число, значит, значение больше искомого. */
43
44const tree = new BinarySearchTree(14, comparator);
45tree.insert(9);
46tree.insert(124);
47tree.insert(3);
48tree.insert(19);
49tree.insert(45);
50tree.insert(1);
51tree.insert(8);
52tree.insert(59);

Все новые значения больше корня уходят в левую ветвь, меньше в правую. Поэтому в примере выше должно получится такое дерево:

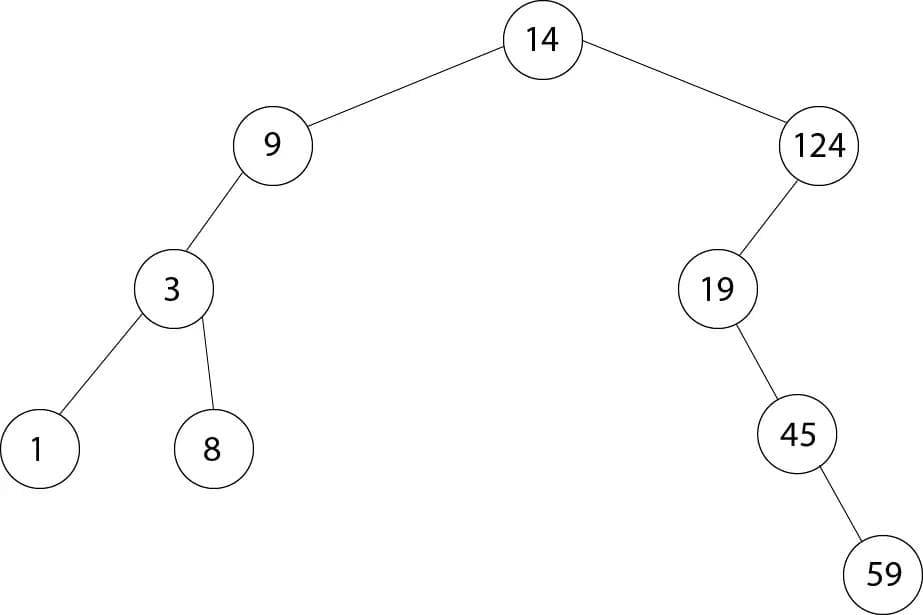
Удаление элемента

Чтобы удалить узел d, нужно найти его в дереве и затем выполнить следующее:

у d нет потомков - присвоить null указателю родительского узла, который сейчас ссылается на d;
у d есть один потомок - этот потомок занимает место d;
у d два потомка - найти следующий по порядку узел (минимальный узел в правом поддереве удаляемого узла) и поставить его на место d.

JavaScript

1//Добавляем в class BinarySearchTreeNode вспомогательные методы
2class BinarySearchTreeNode extends BinaryTreeNode {
3	// ...
4
5	//ищет минимальный элемент в поддереве
6	findMin() {
7		if (!this.left) {
8			return this;
9		}
10
11		return this.left.findMin();
12	}
13
14	// удаляет указанный элемент, если он является дочерним для данного узла.
15	removeChild(nodeToRemove) {
16		if (this.left && this.left === nodeToRemove) {
17			this.left = null;
18			return true;
19		}
20
21		if (this.right && this.right === nodeToRemove) {
22			this.right = null;
23			return true;
24		}
25
26		return false;
27	}
28
29	// заменяет дочерний элемент на новый.
30	replaceChild(nodeToReplace, replacementNode) {
31		if (!nodeToReplace || !replacementNode) {
32			return false;
33		}
34
35		if (this.left && this.left === nodeToReplace) {
36			this.left = replacementNode;
37			return true;
38		}
39
40		if (this.right && this.right === nodeToReplace) {
41			this.right = replacementNode;
42			return true;
43		}
44
45		return false;
46	}
47}
48
49// В class BinarySearchTree добавляем метод remove
50class BinarySearchTree {
51	//...
52
53	remove(value) {
54		const nodeToRemove = this.find(value);
55
56		if (!nodeToRemove) {
57			throw new Error("Item not found");
58		}
59
60		const parent = nodeToRemove.parent;
61
62		// Нет потомков, листовой узел
63		if (!nodeToRemove.left && !nodeToRemove.right) {
64			if (parent) {
65				// Удалить у родителя указатель на удаленного потомка
66				parent.removeChild(nodeToRemove);
67			} else {
68				// Нет родителя, корневой узел
69				nodeToRemove.value = undefined;
70			}
71		}
72
73		// Есть и левый, и правый потомки
74		else if (nodeToRemove.left && nodeToRemove.right) {
75			// Ищем минимальное значение в правом поддереве
76			// И ставим его на место удаляемого узла
77			const nextBiggerNode = nodeToRemove.right.findMin();
78
79			if (this.comparator(nextBiggerNode, nodeToRemove.right) === 0) {
80				// Правый потомок одновременно является минимальным в правом дереве
81				// то есть у него нет левого поддерева
82				// можно просто заменить удаляемый узел на его правого потомка
83				nodeToRemove.value = nodeToRemove.right.value;
84				nodeToRemove.setRight(nodeToRemove.right.right);
85			} else {
86				// Удалить найденный узел (рекурсия)
87				this.remove(nextBiggerNode.value);
88				// Обновить значение удаляемого узла
89				nodeToRemove.value = nextBiggerNode.value;
90			}
91		}
92
93		// Есть только один потомок (левый или правый)
94		else {
95			// Заменить удаляемый узел на его потомка
96			const childNode = nodeToRemove.left || nodeToRemove.right;
97
98			if (parent) {
99				parent.replaceChild(nodeToRemove, childNode);
100			} else {
101				this.root = childNode;
102			}
103		}
104
105		// Удалить ссылку на родителя
106		nodeToRemove.parent = null;
107
108		return true;
109	}
110}
111

Сбалансированные деревья двоичного поиска

Двоичное дерево поиска с автоматической балансировкой - это дерево, которое автоматически сохраняет небольшую высоту (по сравнению с количеством требуемых уровней) независимо от добавления или удаления узлов.

Его высота может быть больше минимальной, но при этом составит Θ(lg n).

Красно-черное дерево — Все ключи хранятся во внутренних узлах, а листья — это нулевые узлы. Каждый узел должен быть красным или черным: корень и все листья — черными, потомки красного узла — черными. Каждый путь от узла к листу должен содержать одинаковое количество черных узлов. Путь от корня до самого дальнего листа не более чем в два раза превышает длину пути от корня до ближайшего листа, поскольку кратчайший возможный путь — это все черные узлы, а в самом длинном из возможных путей красные и черные узлы чередуются, поэтому ни один путь не может быть более чем в два раза длиннее другого.
Косое дерево
декартово дерево (treaps).

Другие посты

Ничего не найдено